1.. Chemical A is converted into another chemical reaction. The rate at which chemical A is being converted is directly proportional to the amount present at any time. Initially 100g of chemical A was present. After 5 minutes, 90 g of A is present.

a) Form a differential equation for the chemical reaction.

b) By solving the differential equation formed in (a), determine the

i) amount of chemical A present after 20 minutes.

ii) time taken for the amount of chemical A to be reduced to 20g.

 

2. The table below shows the prices in US dollars and weights of the five components of an engine, in 1998 and 2005.

COMPONENT	A	B	C	D	E
PRICE ($) 1998	35	70	43	180	480
PRICE ($) 2005	60	135	105	290	800
WEIGHT	6	5	3	2	1

Taking 1998 as the base year,

a) Calculate for 2005 the:

i) simple aggregate price index.

ii) price relative of each component.

iii) weighted aggregate price index.

b) Estimate the cost of an engine in 1998 given that its cost in 2005 was 1600 US dollars.

3. The table below shows the oral interview rank (X) and written interview rank (Y) for 12 candidates.

Candidate	A	B	C	D	E	F	G	H	I	J	K	L
Oral Interview Rank (X)	8	10	9	4	12	5	11	7	3	6	1	2
Written Interview Rank (Y)	11	12	9	7	10	6	8	5	2	4	1	3

Calculate Spearman’s rank correlation coefficient and comment on your result.

4. The sum to infinity of a Geometric Progression (GP) is 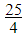 and the first term is 5. Find the

a) common ratio of the GP.

b) sum of the first ten terms of the GP.

5. The table below shows the number of crates of soda sold by a certain shop in 2010.

MONTH	JAN	FEB	MAR	APR	MAY	JUN	JULY	AUG	SEPT	OCT	NOV	DEC
NUMBER OF CRATES	175	783	351	228	378	297	823	338	230	391	410	742

Calculate the four – month moving averages for the data.

5. Determine the coordinates of the stationary point of the curve.

y = ¼ x² – 2x – 5

6. Two independent events A and B are such that P(A)= ¼ and P(B) = ⅗. Find P (A∪B).

7. Given the matrices

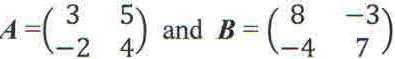, find

a) matrix C such that 3A – 2C + B = I, where I is a 2×2 identify matrix.

b) the determinant of C.

8. A car of mass 2000 kg ascends an incline of sin-1 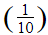 to the horizontal. The resistance force to the motion of the car is 1000 N. The power of the car engine is 59,200W. Calculate the maximum speed of the car.

9. The table below shows a frequency distribution of marks scored by 55 students in a test.

Marks	10-	20-	30-	40-	50-	60-	70-	80-≤ 90
Number of students	2	6	12	15	10	6	3	1

a) Draw a histogram for the data and use it to estimate the modal mark.

b) Calculate the

i) mean mark.

ii) standard deviation.

 

10. Given that (x+1)and (x -2) are factors of the polynomial

ax³ – 3x² – bx + 2, find the values of a and b.

 

 

12. a) Solve the equation 1 + cosɵ= 2 sin²ɵ for values of ɵ between 0⁰ and 360⁰.

b) By eliminating ɵ from the equations x =asecɵ and y=b + C cos ɵ, show that x( y-b)= Ca.

13. A random variable X has a probability density function f(x), defined by

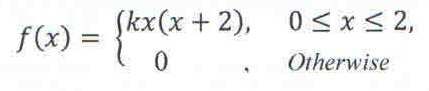
where k is a constant.

Determine the

a) value of k

b) P (1 ≤ X≤1.5)

c) Expectation, E(X)

d) Variance, Var (X)

14. A car initially at rest accelerated uniformly to a speed of 20ms^-1 in 16 seconds. The car then travelled at the attained speed for 2 minutes. The car then accelerated uniformly at 2.5ms^-2 for 8 seconds. It finally decelerated uniformly at 2.5ms^-2 to rest.

a) Find the

i) greatest speed attained by the car.

ii)total time taken by the car to come to rest.

b) Sketch the velocity – time graph for the motion of the car.

c) Use your graph to find the total distance travelled by the car.

END