1. The figure below shows a circle with centre O and angle BCD = 350
Calculate;
a) angle CDB
b) angle ADB
2. Solve the quadratic equation: p2 – 7p + 12 = 0
3. Ben is twice as old as Grace. After four years, the sum of their ages will be 26years. Find Grace’s age.
4. The length of 8 trousers in centimeters are 90, 115, 98, 103, 108, 105, 101 and 98.
Find the;
a) modal length
b) median length
5. Given that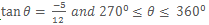 
, determine the value of cos θ.
6. Factorize completely the following expressions:
a) ( a +1)2 -3(a+1)
b) 49 – (x -4)2
7. A square of area 36cm2 is transformed to an image using the matrix 
. Determine the area of the image.
8. Given that 
, find the values of x and y
9. Solve the simultaneous equations
2y – 3x = 13
3y + x = 3
10. The table below shows the ages in years of 40 teachers in a school
|
Age (years) |
30- 34 |
35 -39 |
40 -44 |
45- 49 |
50 - 54 |
55-59 |
60-64 |
65-69 |
|
Numbers of teachers |
2 |
4 |
8 |
10 |
7 |
5 |
3 |
1 |
Draw a cumulative frequency curve (ogive) for the data.
11. Lwegaba stays 6km away from the factory where he works. One day, he started on his journey at 6:42am and arrived at 7:30am. He walked part of the journey at 5km/h. Realizing he would be late, he ran the rest of the journey at 10km/h.
a) What distance did he have to run?
b) The factory closes its gate to its workers at 7:45am. Determine the number of minutes by which Lwegaba would have been late had he not run part of the journey.
12. a) Given the matrices
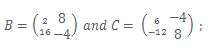
Find the inverse of the matrix (B +C).
b) Mayo sells shirts of sizes Small (S), Medium (M) and extra Large (XL). The table below shows his sales for 3 days.
|
SIZE |
Day |
||
|
Mon |
Tues |
Wed |
|
|
S |
2 |
2 |
1 |
|
M |
7 |
4 |
1 |
|
XL |
3 |
5 |
3 |
He sells each shirt at Shs 40,000 for S, Shs 50,000 for M and Shs 60,000 for XL.
i) Write down a:
- 3 x 3 matrix for sales
- 1 x 3 matrix for prices of the shirts
ii) Use the matrices to calculate his total income from the shirts.
13. On a farm, there are four houses P, Q, R and S. P is 800m on a bearing of 0200 from Q.R is 500m on a bearing of 1600 from Q.S is 1200m on a bearing of 0450 from R.
a) Use a scale of 1c, to represent 100m to construct a scale drawing showing the positions of the four houses.
b) Find the distance and bearing of S from P
14. a) A bag contains red balls and white balls. The probability of picking a white ball is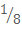
. If there are 24 balls in the bag, find the number of red balls.
b) A basket contains 30 bananas. Ten of them are ripe and the rest are unripe. Two bananas are selected at random from the basket with replacement. Find the probability that;
i) both are ripe
ii) one is ripe and one is unripe
15. The height y meters of wave on a certain day is given by y=5 + cos (30x)0 where x is the number of hours after midnight.
a) Use x at intervals of one hour from 0 to 6 hours to find the corresponding values of y. Put the values of x and y in a table.
b) Use the table to draw a graph of y against x
c) From your graph, find the;
i) height of the wave at 3:30am
ii) time when the height of wave is 5.2m
16. A triangle ABC with vertices A(-4,2) , B(-5,5) and C(-1,4) is mapped onto triangle A’B’C’ by a transformation matrix 
The triangle A’B’C’ is mapped onto triangle A”B”C” by another transformation matrix 
a) Determine the coordinates of the vertices
i) A’B’ and C’
ii) A”B” and C”
b) On the same axes draw the triangles ABC, A’B’C’ and A”B”C”.
c) Describe fully the transformation representedby
i) T
ii) M
17. A school has organized a Geography study tour for 90 students. Two types of vehicles are needed; taxis and costa buses. The maximum capacity of the taxi is 15 passengers while that of the costa bus is 30 passengers. The number of taxis will be greater than the number of costa buses. The number of taxis will be less than five. The cost of hiring a taxi is Shs60,000 while that of the costa is Shs100,000. There is only Shs600000 available.
a) If x represents the number of taxis and y the number of costa buses; write six inequalities for the given information
b) Represent the inequalities on graph paper by shading the unwanted regions (Use the scale of 2cm of 1c unit on bith axes)
c) Find from your graph the number of taxis and costa buses which are full to capacity that must be ordered so that all the students are transported.
END