Answer all questions in this section
1. Given that evaluate 6* (3*1)
6* (3*1)
2. Find the integral values of y in the inequality 2y + 3 < 27 if y >9.
3. Determine the inverse 
4. The ages in years of six girls are as follows: 17, 8,15,12,15,13. What would be the age of the seventh girl that would make the mean age of all the girls to be 13 years?
5. Factorise 3x4 – 48y4 completely.
6. Form a quadratic equation in x whose roots are -3 and ¼
7. The triangles ABC and PQR shown below are similar

Find the lengths of
a) PQ
b) BC
8. A point A(2,5) is reflected in the line y=x which is shown on the graph
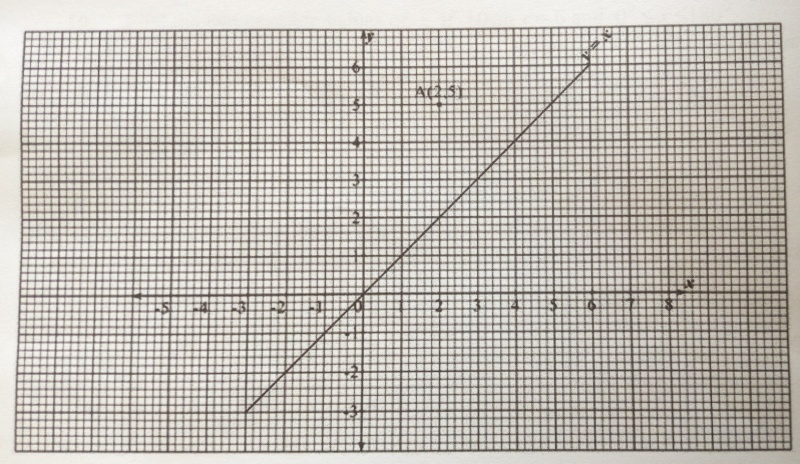
a) Use the graph to show A1 the image A.
b) State the coordinates of A1.
9. The table below shows the sum of two numbers
|
+ |
1 |
2 |
3 |
|
3 |
- |
5 |
6 |
|
5 |
6 |
- |
8 |
|
7 |
8 |
- |
- |
b) What is the probability that the sum is both odd and prime?a) Copy and complete the table
10. Find the two possible values of x if 10sin x=6 and 
SECTION B
Answer any five questions from this section. All questions carry equal marks
11. A bag contains 3 black balls, 4 green balls and 5 yellow balls.
a) If two balls are picked at random without replacement, find the probability that both balls are of the same colour.
b) How many black black balls must be added to the bag so that the probability of drawing a black ball is ½?
12. a) Make N the subject of the expression
V = MN2 P
Hence, find the vale of N when M=9, P= 3 and V = 243.
b) Amooti bought three books and five pens at Shs9700. If he had bought two books and eight pens, he would have spent Shs900 less. Calculate the cost of a
i) book
ii) pen
13. The verticles R(0,1), S(0,3) and T(3,1) of a triangle are mapped onto  by a transformation matrix
by a transformation matrix
a) Find the coordinates of the image triangle 
b) Use the determinant of P to find the ratio of the area of triangle RST to the area of triangle  .
.
c) Determine the matrix of transformation which maps  back onto RST
back onto RST
14. Using a ruler, a pencil and a pair of compasses only
a) construct a triangle ABC, in which angle BAC = 300, angle ABC is 1200 and = 8cm.
b) Measure and record the lengths AC and BC
c) i) Draw an inscribed circle in the triangle ABC
ii) Measure and record the radius of the circle.
15. a) Copy and complete the table below for values 10-x2
|
x |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
10-x2 |
-6 |
|
6 |
9 |
10 |
9 |
|
1 |
-6 |
i) Using 2cm for 1 unit on the x-axis and 1cm for1 unit on the y- axis, draw the graph of y = 10-x2
ii) Use your graph to solve the equation 10-x2 =0.
b)i) On the same axes, draw the graph of the equation y = 2x +3
ii) Use your graphs to solve the equation x2 +2x -7 = 0
16. a) Using matrix method, solve the following simultaneous equations
3x-4y-1 =0
6x – 6y =5
b) Three girls went shopping and bought loaves of bread, cakes and packets of biscuits. Ann bought 2 loaves, 3 cakes and 6 packets of biscuits. Betty bought 3 loaves, 4 cakes and 5 packets of biscuits. Caroline bought 3 loaves, 6 cakes and 3 packets of biscuits.
i) Represent this information in matrix form.
ii) One loaf cost Shs3,500, one cake costs Shs500 and a packet of biscuits costs Shs2,000. Using matrix multiplication obtain the money spent by each girl. Hence, determine the total amount spent by the three girls.
17. A wholesaler wishes to transport at least 240 bags of sugar from the factory to his shop. He has a lorry that can carry 90 bags per trip and a pick-up that can carry 20bags per trip. The cost of each trip is Shs 50,000 for the lorry and Shs 15,000for a pick-up. He has Shs180,000 available to transport the sugar. The pick-up makes more trips than the lorry. If x is the number of trips to be made by the lorry and y the number of trips to be made by the pick-up;
a) Write down five inequalities to represent the given information
b) Represent the inequalities on a graph
c) Use the graph to find the possible number of trips to be made by the lorry and the pick-up. Hence find the minimum cost of transporting the bags of sugar.
